Kümelerde Birleşim ve Kesişim İşlemleri Soruları ve Çözümleri 9. Sınıf
Bu yazımızda Kümelerde Birleşim ve Kesişim İşlemleri çözümlü soruları yer almaktadır. Konu hakkında bilgi eksiğiniz varsa öncelikle Kümelerde Birleşim ve Kesişim İşlemleri Konu Anlatımı yazımıza göz gezdirebilirsiniz.
Çözümlü Örnek Test Soruları: Kümelerde Birleşim ve Kesişim İşlemleri
Soru 1:
A = {1, 2, 3} ve B = {2, 3, 4} kümeleri verilmiştir. A ∪ B birleşim kümesi nedir?
A) {1, 2, 3}
B) {2, 3}
C) {1, 2, 3, 4}
D) {1, 4}
Cevap: C
Çözüm: Birleşim işlemi, iki kümenin tüm elemanlarını içerir.
A ∪ B = {1, 2, 3, 4}.
Soru 2:
A = {a, b, c} ve B = {b, c, d} kümeleri verilmiştir. A ∩ B kesişim kümesi nedir?
A) {a, d}
B) {b, c}
C) {a, b, c, d}
D) {a, b}
Cevap: B
Çözüm: Kesişim işlemi, iki kümenin ortak elemanlarını içerir.
A ∩ B = {b, c}.
Soru 3:
A = {1, 2, 3, 4} ve B = {3, 4, 5} kümeleri verilmiştir. A ∪ B ve A ∩ B işlemlerinin sonuçlarının toplam eleman sayısı kaçtır?
A) 5
B) 6
C) 7
D) 8
Cevap: C
Çözüm:
Birleşim kümesi: A ∪ B = {1, 2, 3, 4, 5} → 5 eleman
Kesişim kümesi: A ∩ B = {3, 4} → 2 eleman
Toplam eleman sayısı: 5 + 2 = 7.
Soru 4:
A = {x | x bir doğal sayı ve x ≤ 5}, B = {x | x tek sayı ve x ≤ 7}. A ∩ B nedir?
A) {1, 3, 5}
B) {2, 4}
C) {1, 2, 3, 5}
D) {1, 3, 5, 7}
Cevap: A
Çözüm:
A = {0, 1, 2, 3, 4, 5}, B = {1, 3, 5, 7}
A ∩ B = {1, 3, 5} (ortak elemanlar).
Soru 5:
Evrensel küme E = {1, 2, 3, 4, 5, 6} ve A = {2, 4, 6} verildiğinde, A’nın tümleyeni A’ nedir?
A) {2, 4, 6}
B) {1, 3, 5}
C) {1, 2, 3, 4, 5}
D) {1, 2, 3, 4, 6}
Cevap: B
Çözüm:
A’nın tümleyeni, evrensel kümede A’nın dışında kalan elemanlardır:
A’ = {1, 3, 5}.
Soru 6:
A = {1, 2, 3} ve B = {3, 4, 5} kümeleri için A ∪ B ve A ∩ B sonuçları verilmiştir.
A ∪ B = {1, 2, 3, 4, 5}, A ∩ B = {3}.
(A ∪ B) – (A ∩ B) nedir?
A) {1, 2, 4, 5}
B) {3}
C) {1, 2, 3, 4, 5}
D) {1, 2}
Cevap: A
Çözüm:
(A ∪ B) – (A ∩ B) işleminde birleşim kümesinden kesişim kümesi çıkarılır.
{1, 2, 3, 4, 5} – {3} = {1, 2, 4, 5}.
Örnek: A = {a, b, c} ve B = {c, d, e) kümeleri veriliyor. A ∪ B kümesini oluşturarak şema yöntemi ile gösterelim.
Çözüm: A ve B kümesindeki tüm harflerle yeni bir küme oluşturursak; A ∪ B = {a, b, c, d, e} olacaktır. Küme içerisinde her elemanın yalnız bir kez yazıldığını unutmayalım. A ∪ B kümesini şema ile gösterin.
Örnek: A = {a, b, c, 1, 2} ve B = {2, 3, c, d} kümeleri veriliyor. A ∩ B kümesini oluşturarak şema yöntemi ile gösterelim.
Çözüm: A = {a, b, c, 1, 2} ve B = {2, 3, c, d} olduğundan her iki kümenin ortak elemanları c ve 2 dir. O halde, A ∩ B = {c, 2} olacaktır. Şema yöntemi ile gösterin.
Örnek: A = {MEHMET kelimesinin harfleri}
B = {MERMER kelimesinin harfleri}
C = {EMİR kelimesinin harfleri} olarak veriliyor. A ∩ B ∩ C kümesini oluşturarak şema ile gösterelim.
Çözüm: A = {M, E, H, T} B = {M, E, R} C = {E, M, İ, R} dir.
A ∩ B ∩ C kümesi her üç kümede de ortak olarak bulunan elemanların kümesidir. Görüldüğü gibi her üç kümede M ve E elemanları mevcuttur. O halde A ∩ B ∩ C = {M, E} olacaktır. Şema gösterimini yapınız.
Örnek: A = {1, 2, 3) ve A ∪ B = {1, 2, 3, 4, 5} olduğuna göre, B kümesi aşağıdakilerden hangisi olamaz?
A) {4, 5} B) {1, 3, 4, 5} C) {1, 2, 3, 4}
D) {2, 4, 5} E) {1, 2, 4, 5}
Çözüm: A = {1, 2, 3} ve A ∪ B = {1, 2, 3, 4, 5} olduğundan B kümesinde 4 ve 5 elemanlarının mutlaka bulunması gerekir. O halde, B kümesi {1, 2, 3, 4} olamaz. Doğru cevap “C” seçeneğidir.





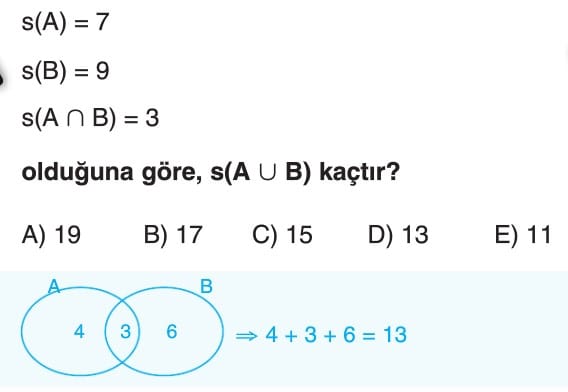
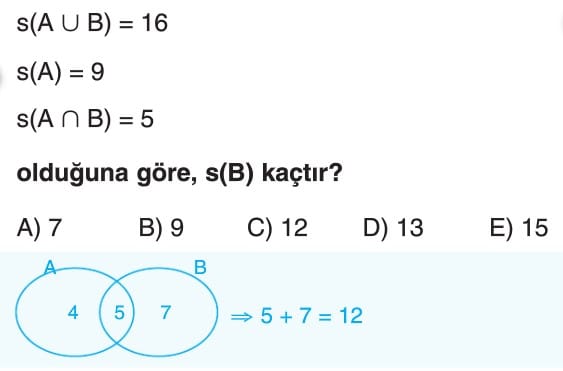



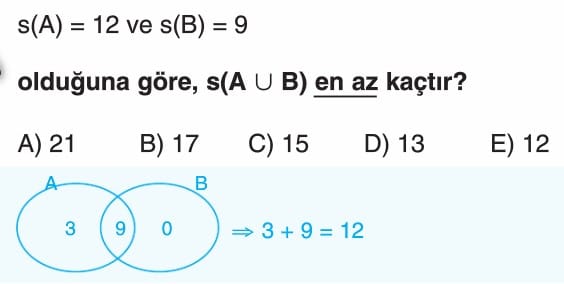
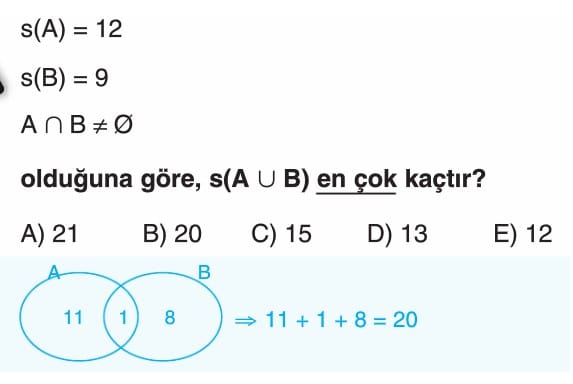
















Baya iyi anlatinoz